The Most Important Number to Know About Your Portfolio
And you've probably never thought about it.
The secret to investing is Compounding.
It’s what happens when you put your money to work and tell it to go make you some more money.
It’s exponential growth.
It’s your money going viral.
And it works for you even when you’re sleeping.
For all that, it’s likely you don’t hear investors or “experts” talk much about Compounding?
Why?
Because it takes Time. (Time, by the way, is the most important factor in investing.)
If you scanned the articles in any edition of the Wall Street Journal (or any other financial information provider), you’d find little coverage of Compounding.
Do you remember the last time you spoke to your financial advisor? Did you talk about Compounding?
Probably not, but you should.
Why Does it Matter?
Still, you’ve probably at least heard about Compounding and know—if only vaguely—that it’s important.
A simple example might help to clarify.
Let’s say you made a one-time investment of $10,000 that grows by 3% every year. We want to know what it would be worth at the end of 40 years.
Here goes. After 1 year, your investment will have grown by $300 (3% x $10,000) to $10,300.
Not too exciting.
In year 2, however, you earn $309 (3% x $10,300).
Because your balance was higher, you earned more—an additional $9—for year 2, and your investment is now worth $10,609.
Still nothing to write home about.
If you’re told Compounding is so wonderful, you can start to see why you’re a bit skeptical after 2 years.
If we skip forward to year 10, however, your investment is now worth about $13,000 (from here on out, we’re going to round to the nearest thousandth).
After 20 years, it’s worth $18,000.
After 30 years, it’s worth $24,000.
Finally, after 40 years, it’s worth $33,000.
You’ve more than tripled your money, but let’s face it, it took a long time, and it hardly seems magical.
What’s the Problem?
So, what’s the problem? Investing at 3% hardly made you rich. It may have helped you keep up with inflation, but that’s about it.
What could you do differently?
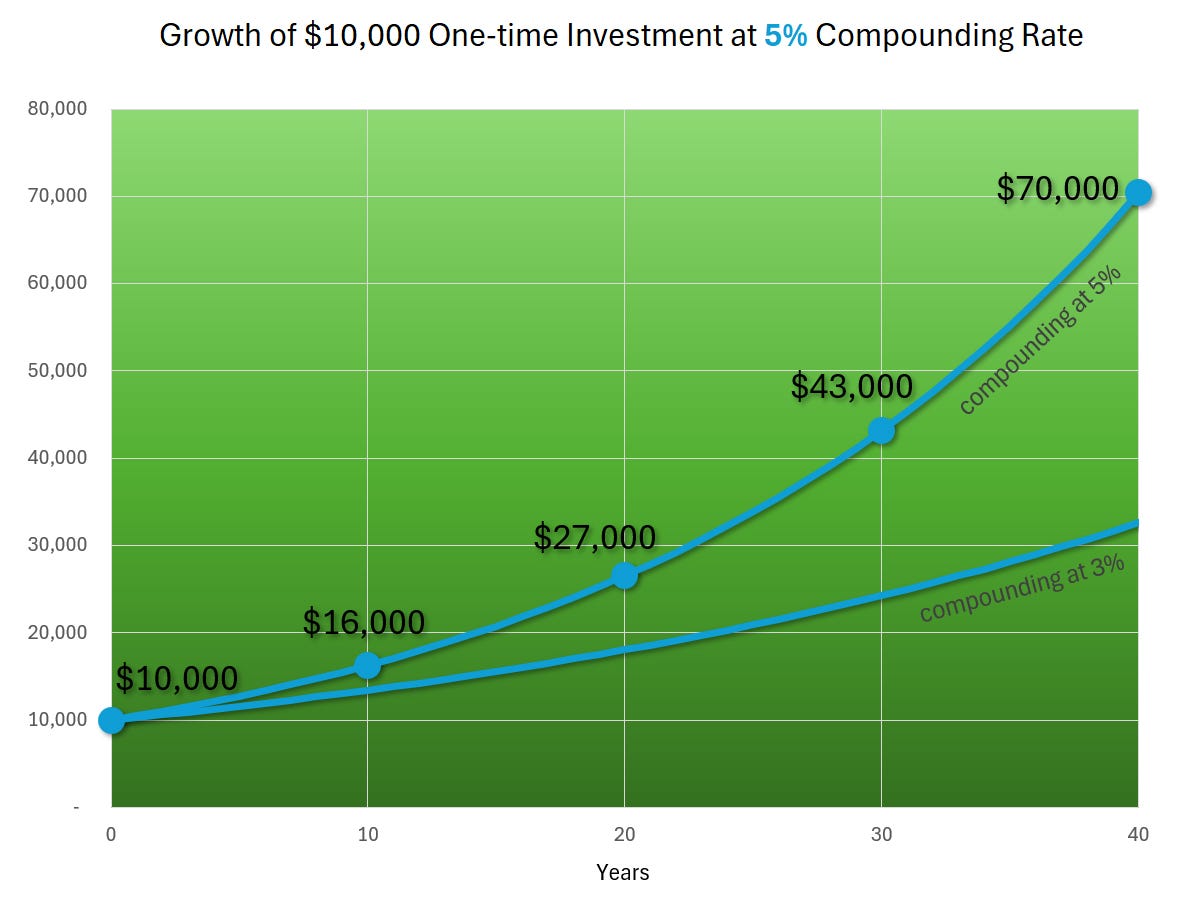
Maybe the 3% rate was too low. What if you grew your investment at 5% per year?
Before we look at the numbers, what’s your guess of the value at the end of 40 years?
Remember, it was $33,000 when growing at 3%.
Perhaps you might think that since we increased the rate from 3% to 5%—a 66.7% increase—that the value would be $54,000 (which is 66.7% higher).
Let’s see.
1 Yr: $10,500
10 Yrs: $16,000
20 Yrs: $27,000
30 Yrs: $43,000
40 Yrs: $70,000
Something weird—but good—is going on.
We didn’t double the rate, but we more than doubled the value at the end of 40 years.
This is exponential growth, i.e., Compounding, in action, and things are starting to get a bit more interesting.
But still not quite life-changing.
Let’s Crank it Up to 10!
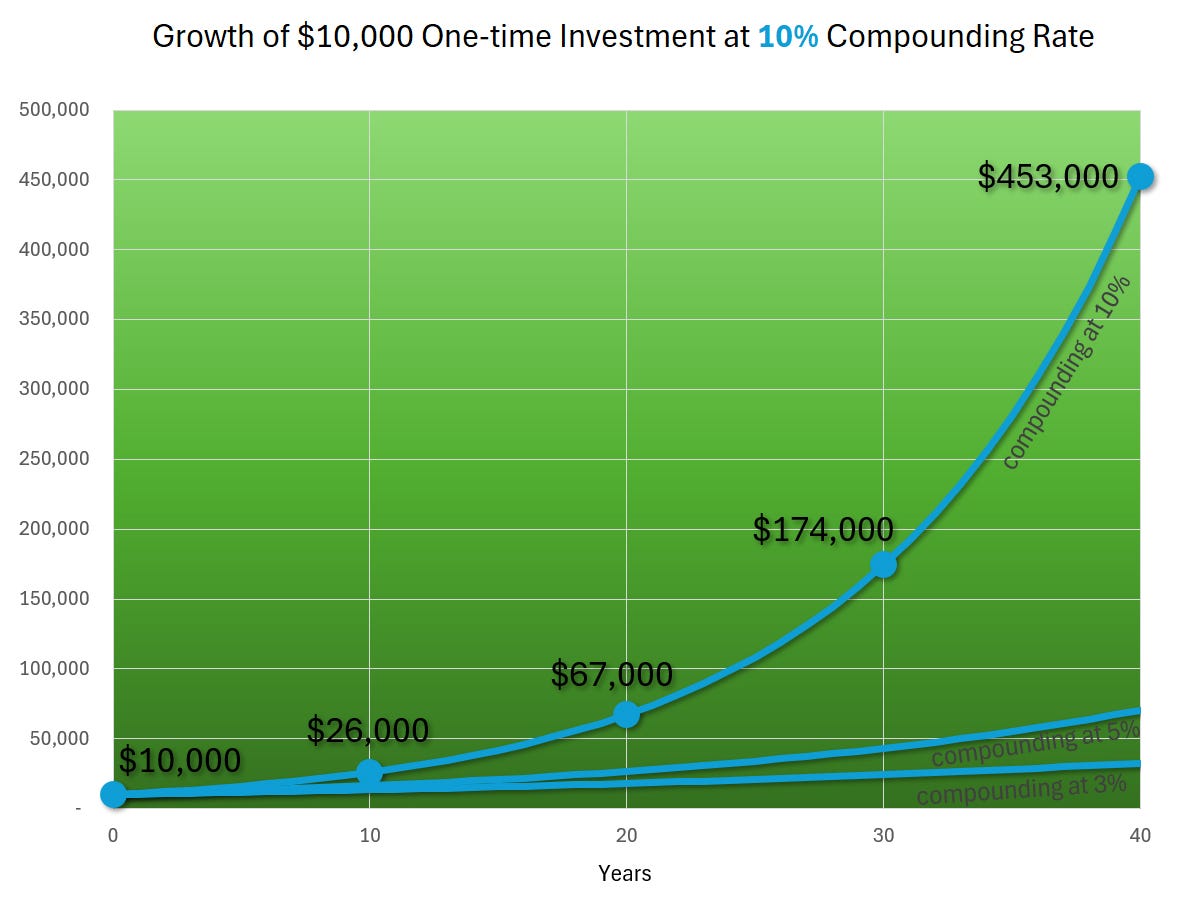
What if we increased the rate to 10%?
Here are the numbers:
1 Yr: $11,000
10 Yrs: $26,000
20 Yrs: $67,000
30 Yrs: $174,000
40 Yrs: $453,000
This is significant. A one-time investment of $10,000 grows to around $453,000 in 40 years.
And if, in a nod to Spinal Tap, we took it to 11, the value would be $650,000!
Every 1% increase in the Compounding Rate makes an incredible difference.
Ten More Years
We used 40 years because it’s the typical amount of time someone might work and invest for retirement.
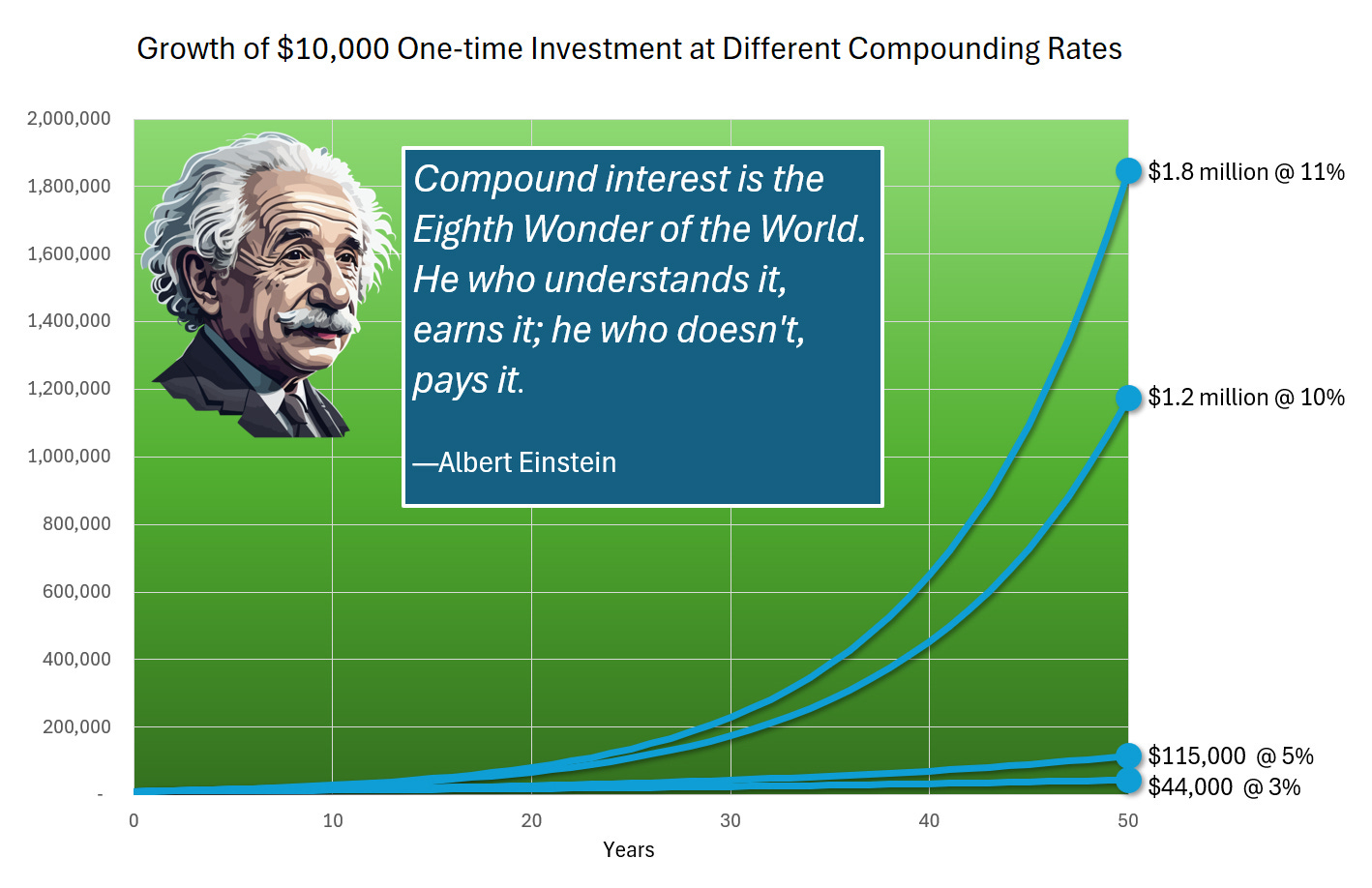
But you don’t stop investing when you reach retirement, so how do the numbers look if we compound for 50 years (still using a one-time investment of $10,000)?
3% for 50 years: $44,000
5% for 50 years: $115,000
10% for 50 years: $1.2 million
11% for 50 years: $1.8 million
These numbers with the higher compounding rates are beginning to get mind-boggling.
Compounding even impressed Albert Einstein, who is often attributed with calling it the Eighth Wonder of the World.
What We Didn’t Cover (Yet)
Compounding is the secret to investing, but it takes two things in order for the magic to work: Time and a sufficiently high Compounding Rate.
The obvious next question is: Which investments can generate these types of compounding rates?
What happens when you make regular investments over time (like in your 401(k) plan) instead of a one-time investment?
And what about volatility?
We’ll cover these in next week’s post.
We’ll leave you with this: Do you know the long-term Compounding Rate of your portfolio?
Best regards,
Stuart & Sharon